Computers know nothing but numbers. As humans we have varying levels of skill in using numbers, but most of the time we’re communicating with words and phrases. So in the early days of computing, the earliest software developers had to find a way to map each character—a letter Q, the character #, or maybe a lowercase b—into a number. A table of characters would be made, usually either 128 or 256 of them, depending on whether data was stored or transmitted using 7 or 8 bits. Often the data would be stored as 7 bits, so that the eighth bit could be used as a parity bit, a simple method of error correction (because data transmission—we’re talking modems and serial ports here—was so error prone).

Early on, such encoding systems were designed in isolation, which meant that they were rarely compatible with one another. The number 34 in one character set might be assigned to “b”, while in another character set, assigned to “%”. You can imagine how that works out over an entire message, but the hilarity was lost on people trying to get their work done.

In the 1960s, the American National Standards Institute (or ANSI) came along and set up a proper standard, called ASCII, that could be shared amongst computers. It was 7 bits (to allow for the parity bit) and looked like:

  0 nul    1 soh    2 stx    3 etx    4 eot    5 enq    6 ack    7 bel
  8 bs     9 ht    10 nl    11 vt    12 np    13 cr    14 so    15 si
 16 dle   17 dc1   18 dc2   19 dc3   20 dc4   21 nak   22 syn   23 etb
 24 can   25 em    26 sub   27 esc   28 fs    29 gs    30 rs    31 us
 32 sp    33  !    34  "    35  #    36  $    37  %    38  &    39  '
 40  (    41  )    42  *    43  +    44  ,    45  -    46  .    47  /
 48  0    49  1    50  2    51  3    52  4    53  5    54  6    55  7
 56  8    57  9    58  :    59  ;    60  <    61  =    62  >    63  ?
 64  @    65  A    66  B    67  C    68  D    69  E    70  F    71  G
 72  H    73  I    74  J    75  K    76  L    77  M    78  N    79  O
 80  P    81  Q    82  R    83  S    84  T    85  U    86  V    87  W
 88  X    89  Y    90  Z    91  [    92  \    93  ]    94  ^    95  _
 96  `    97  a    98  b    99  c   100  d   101  e   102  f   103  g
104  h   105  i   106  j   107  k   108  l   109  m   110  n   111  o
112  p   113  q   114  r   115  s   116  t   117  u   118  v   119  w
120  x   121  y   122  z   123  {   124  |   125  }   126  ~   127 del

The lower numbers are various control codes, and the characters 32 (space) through 126 are actual printed characters. An eagle-eyed or non-Western reader will note that there are no umlauts, cedillas, or Kanji characters in that set. (You’ll note that this is the American National Standards Institute, after all. And to be fair, those were things well outside their charge.) So while the immediate character encoding problem of the 1960s was solved for Westerners, other languages would still have their own encoding systems.

As time rolled on, the parity bit became less of an issue, and people were antsy to add more characters. Getting rid of the parity bit meant 8 bits instead of 7, which would double the number of available characters. Other encoding systems like ISO-8859-1 (also called Latin-1) were developed. These had better coverage for Western European languages, by adding some umlauts we’d all been missing. The encodings kept the first 0–127 characters identical to ASCII, but defined characters numbered 128–255.

However this still remained a problem, even for Western languages, because if you were on a Windows machine, there was a different definition for characters 128–255 than there was on the Mac. Windows used what was called Windows 1252, which was just close enough to Latin-1 (embraced and extended, let’s say) to confuse everyone and make a mess. And because they like to think different, Apple used their own standard, called Mac Roman, which had yet another colorful ordering for characters 128–255.

This is why there are lots of web pages that will have squiggly marks or odd characters where em dashes or quotes should be found. If authors of web pages include a tag in the HTML that defines the character set (saying essentially “I saved this on a Western Mac!” or “I made this on a Norwegian Windows machine!”) then this problem is avoided, because it gives the browser a hint at what to expect in those characters with numbers from 128–255.

Those of you who haven’t fallen asleep yet may realize that even 200ish characters still won’t do—remember our Kanji friends? Such languages usually encode with two bytes (16 bits to the West’s measly 8), providing access to 65,536 characters. Of course, this creates even more issues because software must be designed to no longer think of characters as a single byte.

In the very early 90s, the industry heavies got together to form the Unicode consortium to sort out all this encoding mess once and for all. They describe their charge as:

Unicode provides a unique number for every character,
no matter what the platform,
no matter what the program,
no matter what the language.

They’ve produced a series of specifications, both for a wider character set (up to 4! bytes) and various methods for encoding these character sets. It’s truly amazing work. It means we can do things like have a font (such as the aptly named Arial Unicode) that defines tens of thousands of character shapes. The first of these (if I recall correctly) was Bitstream Cyberbit, which was about the coolest thing a font geek could get their hands on in 1998.

The most basic version of Unicode defines characters 0–65535, with the first 0–255 characters defined as identical to Latin-1 (for some modicum of compatibility with older systems).

One of the great things about the Unicode spec is the UTF-8 encoding. The idea behind UTF-8 is that the majority of characters will be in that standard ASCII set. So if the eighth bit of a character is a zero, then the other seven bits are just plain ASCII. If the eighth bit is 1, then it’s some sort of extended format. At which point the remaining bits determine how many additional characters (usually two) are required to encode the value for that character. It’s a very clever scheme because it degrades nicely, and provides a great deal of backward compatibility with the large number of systems still requiring only ASCII.

Of course, assuming that ASCII characters will be most predominant is to some repeating the same bias as back in the 1960s. But I think this is an academic complaint, and the benefits of the encoding far outweigh the negatives.

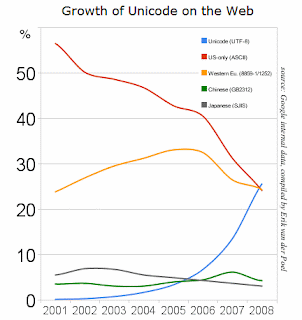Anyhow, the purpose of this post was to write that Google reported yesterday that Unicode adoption on the web has passed ASCII and Western European. This doesn’t mean that English language characters have been passed up, but rather that the number of pages encoded using Unicode (usually in UTF-8 format), has finally left behind the archaic ASCII and Western European formats. The upshot is that it’s a sign of us leaving the dark ages—almost 20 years since the internet was made publicly available, and since the start of the Unicode consortium, we’re finally starting to take this stuff seriously.

The Processing book also has a bit of background on ASCII and Unicode in an Appendix, which includes more about character sets and how to work with them. And future editions of vida will also cover such matters in the Parse chapter.

Kottke and Freakonomics were kind enough to link over here, which has brought more queries about salaryper. Rather than piling onto the original web page, I’ll add updates to this section of the site.

I didn’t include the project’s back story with the 2008 version of the piece, so here goes:

Some background for people who don’t watch/follow/care about baseball:

When I first created this piece in 2005, the Yankees had a particularly bad year, with a team full of aging all-stars and owner George Steinbrenner hoping that a World Series trophy could be purchased for $208 million. The World Champion Red Sox did an ample job of defending their title, but as the second highest paid team in baseball, they’re not exactly young upstarts. The Chicago White Sox had an excellent year with just one third the salary of the Yankees, while the Cardinals are performing roughly on par with what they’re paid. Interestingly, the White Sox went on to win the World Series. The performance of Oakland, which previous years has far exceeded their overall salary, was a story, largely about their General Manager Billy Beane, told in the book Moneyball.

Some background for people who do watch/follow/care about baseball:

I neglected to include a caveat on the original page that this is a really simplistic view of salary vs. performance. I created this piece because the World Series victory of my beloved Red Sox was somewhat bittersweet in the sense that the second highest paid team in baseball finally managed to win a championship. This fact made me curious about how that works across the league, with raw salaries and the general performance of the individual teams.

There are lots of proportional things that can be done too—the salaries especially exist across a wide range (the Yankees waaaay out in front, followed the another pack of big market teams, then everyone else).

There are far more complex things about how contracts work over multiple years, how the farm system works, and scoring methods for individual players that could be taken into consideration.

This piece was thrown together while watching a game, so it’s perhaps dangerously un-advanced, given the amount of time and energy that’s put into the analysis (and argument) of sports statistics.

That last point is really important… This is fun! I encourage people to try out their own methods of playing with the data. For those who need a guide on building such a beast, the book has all the explanation and all the code (which isn’t much). And if you adapt the code, drop me a line so I can link to your example.

I have a handful of things I’d like to try (such as a proper method for doing proportional spacing at the sides without overdoing it), though the whole point of the project is to strip away as much as possible, and make a straightforward statement about salaries, so I haven’t bothered coming back to it since it succeeds in that original intent.

Chapters 9 and 10 (acquire and parse) are secretly my favorite parts of Visualizing Data. They’re a grab bag of useful bits based on many years of working with information (previous headaches)… the sort of things that come up all the time.

Page 327 (Chapter 10) has some discussion about little endian versus big endian, the way in which different computer architectures (Intel vs. the rest of the world, respectively) handle multi-byte binary data. I won’t repeat the whole section here, though I have two minor errata for that page.

First, an error in formatting which lists network byte order, rather than network byte order. The other problem is that I mention that little endian versions of Java’s DataInputStream class can be found on the web for little more than a search for DataInputStreamLE. As it turns out, that was a big fat lie, though you can find a handful if you search for LEDataInputStream (even though that’s a goofier name).

To make it up to you, I’m posting proper DataInputStreamLE (and DataOutputStreamLE) which are a minor adaptation of code from the GNU Classpath project. They work just like DataInputStream and DataOutputStream, but just swap the bytes around for the Intel-minded. Have fun!

DataInputStreamLE.java

DataOutputStreamLE.java

I’ve been using these for a project and they seem to be working, but let me know if you find errors. In particular, I’ve not looked closely at the UTF encoding/decoding methods to see if there’s anything endian-oriented in there. I tried to clean it up a bit, but the javadoc may also be a bit hokey.

(Update) Household historian Shannon on the origin of the terms:

The terms “big-endian” and “little-endian” come from Gulliver’s Travels by Jonathan Swift, published in England in 1726. Swift’s hero Gulliver finds himself in the midst of a war between the empire of Lilliput, where people break their eggs on the smaller end per a royal decree (Protestant England) and the empire of Blefuscu, which follows tradition and breaks their eggs on the larger end (Catholic France). Swift was satirizing Henry VIII’s 1534 decision to break with the Roman Catholic Church and create the Church of England, which threw England into centuries of both religious and political turmoil despite the fact that there was little doctrinal difference between the two religions.

Blake Tregre found a typo on page 55 of Visualizing Data in one of the comments:

// Set the value of m arbitrarily high, so the first value
// found will be set as the maximum.
float m = MIN_FLOAT;

That should instead read something like:

// Set the value of m to the lowest possible value,
// so that the first value found will automatically be larger.
float m = MIN_FLOAT;

This also reminds me that the Table class used in chapter 4, makes use of Float.MAX_VALUE and -Float.MAX_VALUE, which are inherited from Java. Processing has constants named MAX_FLOAT and MIN_FLOAT that do the same thing. We added the constants because -Float.MAX_VALUE seems like especially awkward syntax when you’re just trying to get the smallest possible float. The Table class was written sometime before the constants were added to the Processing syntax, so they use the Java approach.

There is a Float.MIN_VALUE in Java, however the spec does a very unfortunate thing, because MIN_VALUE is defined as “A constant holding the smallest positive nonzero value of type float”, which sounds promising until you realize that it just means a very tiny positive number, not the minimum possible value for float. It’s not clear why they thought this would be a more useful constant (or useful at all).

And to make things even more confusing, Integer.MAX_VALUE and Integer.MIN_VALUE behave more like the way you might expect, where the MIN_VALUE is in fact that the lowest (most negative) value for an int. Had they used the same definition as Float.MIN_VALUE, then Integer.MIN_VALUE would equal 1. Which illustrates just how silly it is to do that for the Float class.